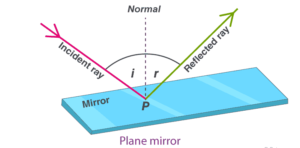
A ray of light hits a surface at a point. From that point the line straight up, at 90 degrees to the surface, is called the normal. The angle between the normal and the ray of light is called the angle of incidence. (read more here)
The incident ray and reflected ray form two angles at the point of incidence:
- The angle formed between the normal and the incident ray at the point of incidence is called the angle of incidence.
- Similarly, the angle formed between the normal and the reflected ray at the point of incidence is called the angle of reflection.
Angle of Incidence Formula
The angle of incidence is equal to the reflected angle through the law of reflection. The angle of incidence and the angle of reflection is always equal, and they are both on the same plane along with the normal.
The relationship between the angle of incidence and angle of refraction is explained by Snell’s law, which states that the ratio of the sine of the angle of refraction and the sine of the angle of incidence is always constant and equivalent to the ratio of phase velocities of the two mediums it is passing through.
The formula for Snell’s Law can also be used to solve for the angle of incidence. By rewriting the equation so the angle of incidence is isolated, the following formula is found:
θ1= arcsin (n2/n1sinθ2)
There is a special case in which the angle of incidence allows light to be refracted at an angle of 90°. This angle is known as the critical angle. The critical angle can be found by plugging in 90° for the angle of refraction and solving for the angle of incidence. Since sin90° is equal to 1. (read more here)
The angle of incidence is equal to the angle of reflection because the light ray selects the shortest path to reach the destination. This behavior of light is known as Fermat’s principle. The same behavior is shown by the light ray when it gets reflected from the plane surface. Therefore, the angle of incidence and the angle of reflection are equal.
More info on Angle of Incidence here
You might also want to read:


